Fibonacci Nedir? Borsada Fibonacci Nasıl Kullanılır?
Fibonacciyi sizlere anlatmadan önce, ünlü matematikçi Leonardo Fibonacci’den bahsetmek şarttır. Çünkü Leonardo Fibonacciyi anlatmadan, fibonacci matematiğinin detaylarına inmek kolay değil. Leonardo Fibonacci, 1170 yılında, İtalya Pisa’da dünyaya gelmiş ve Orta Çağ’ın en yetenekli matematikçisi ünvanıyla yaşamış bir bilim adamıdır.

Fibonacci, modern çağ döneminde Hint – Arap sayılarını Avrupa’ya getirmiş, Liber Abaci isimli matematik kitabını yazmış ve bu kitapta Fibonacci Dizisi olarak adlandırılan sayı dizilerinden bahsetmiştir. Liber Abaci kitabında yazılan satırlardan, “Fibonacci nedir?” sorusuna bir cevap bulabiliriz.
Bu kitapta, bir tavşan nüfusunun büyümesi matematik diliyle açıklanmaya çalışılmış ve Fibonacci, bu büyümeyi hesaplarken, günümüzde Fibonacci Sayı Dizisi olarak adlandırılan sıralı rakamları kullanmıştır. En basit haliyle Fibonacci Nedir sorusuna şöyle cevap verebiliriz:
- Fibonacci sayı dizisinde, her rakam, kendinden önce sıralanmış iki rakamın toplamıdır. Sayılar 0 ve 1 rakamı ile başlar. 0 ve 1’den sonra oluşan ilk rakam yine 1’dir, çünkü 0 ve 1’in toplamı 1’dir. Böylece ilk oluşumda rakamlar şöyle olur:
- 0, 1, 1,
- İşler şimdi daha da ilginçleşmeye başlamıştır. Seriye eklenecek 4. rakam, ondan önceki iki rakamın toplanmasıyla elde edilir. Yukarıdaki örnekde, son rakam 1, ve ondan önceki rakam da 1’dir. İkisinin toplamı 2 olduğu için, serinin sonuna 2 eklenir. Fibonacci Sayı Dizisi şöyle devam eder:
- 0, 1, 1, 2,
- Yine aynı formülle, bu sefer seriye eklenecek yeni rakamı bulabilmek için, serideki son iki rakamı toplamamız gerekir. Bunlar 2 ve 1’dir. Bu ikisinin toplamı 3 olacağı için, seriye 3 eklenir:
- 0, 1, 1, 2, 3,
- Buraya kadar sıralama normal gidiyor gibi gözükse de, fark tam da burada açılmaya başlar çünkü seriye eklenecek yeni rakamı bu sefer son iki rakamın toplamıyla 5 olarak buluruz (2+3=5). Gördüğünüz gibi, sırayla giden rakamlar, son rakamda farkı açtı ve fark ikiye çıktı. Fibonacci Sayı Dizimizin son rakamını sıraya ekleyelim:
- 0, 1, 1, 2, 3, 5
- Mantığı anladığınızı düşünüyorum. Şimdi, devam edersek, fibonacci sayı dizimize ekleyeceğimiz son rakam, kendinden önceki iki rakamın toplanmasıydı. Bu örnekte, yeni rakamımız, 3 ve 5’in toplamı, yani 8 olacaktır. Bunu da fibonacci sayı dizisine eklediğimizde, son güncel dizi şöyle olacaktır:
- 0, 1, 1, 2, 3, 5, 8
Örneği bundan daha fazla ilerletmeye gerek olmadığını varsayalım, çünkü mantığı anladınız. Oluşan her rakam, kendinden önceki iki rakamın toplamından oluşuyor. Yani, mesela, yukarıdaki dizide, 8’in yanına eklenecek rakam, 8+5’in toplamı olacak, yani 13 olacak.
Bu hesaplama ileri doğru gittikçe, rakamlar birbirine katsayı olarak o kadar yaklaşır ki, elimize Altın Oran dediğimiz ve 1.618’i gösteren bir değer çıkar. İşte Fibonacci Nedir sorusunun cevabı aslında bu altın oranda, yani 1.618’de gizlidir.
Şimdi, her bir rakamı, hem kendinden bir önceki, hem de kendinden bir sonraki rakama bölelim. Sonuç şöyle çıkacak:
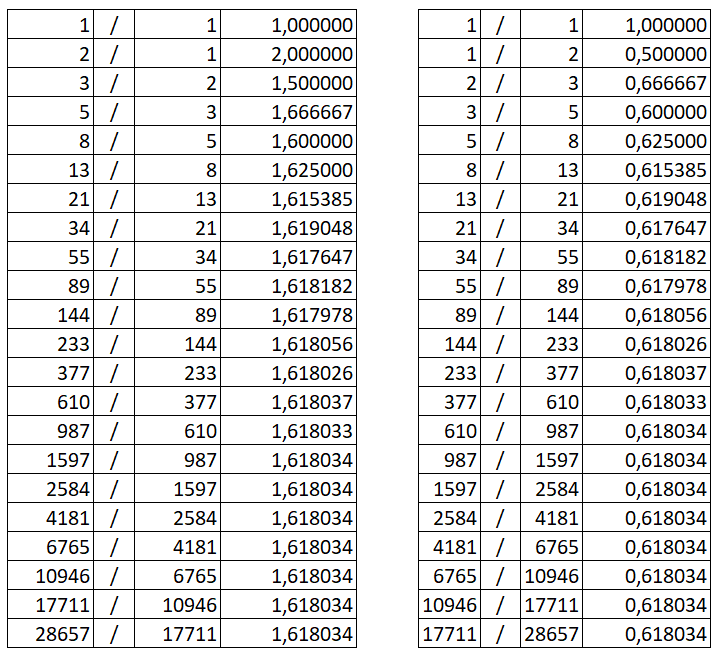
Gördüğünüz gibi, kendinden bir önceki rakama bölünen rakam, büyüdükçe 1.61’e yakınlaşıyor. Kendinden bir sonraki rakama bölünen rakam, büyüdükçe 0.61’e yakınalşıyor.
Dünya üzerinde gördüğünüz çoğu şeyin oranı 1.618’e tekabül eder. Yaşayan çoğu canlının tüm organlarının geometrik oranı, antik mimari eserlerin tasarımları, kar tanelerinin içindeki geometri, Ayçiçeğinin merkezden dışarı doğru tasarımı. Hepsi bu altın orana uygun tasarlanmıştır.
Borsada Fibonacci Nedir, Nasıl Kullanılır?
Fibonacci Nedir sorusunun cevabını aslında Borsa için arıyorsunuz biliyorum. Şimdi biraz borsadan bahsedelim. Borsada her grafik, her fiyat hareketi çeşitli dalgalardan oluşur. İtki dalgası ve Düzeltme dalgası ana dalgalardır. Fibonacci’nin grafiklerde kullanımına göre, her itki dalgasından sonra oluşacak düzeltme dalgası, itki dalgasının altın oranına veya tam sayının bu orana oranına göre şekillenir. Altın oran neydi? 1.61 ve 0.61. O zaman, bir itki dalgasının düzeltmesi de, toplam itki dalgasının %61’ine kadar inebilir. Bu rakamın 1’den çıkarılması bize 0.38’i verir. 0.38 de aynı zamanda başka bir düzeltme dalgası rakamıdır.
Özetle, bir itki dalgasının başlangıcından bitişine kadar çekilen fibonacci düzeltme çizimi, size o itki dalgasının 0.38 ve 0.61’ini verir ve bu iki rakam, düzeltme başladığında fiyatın inebileceği seviyelerdir. Fiyat buralardan alıcı bulur ve yukarı doğru ilerler.
Bu konuyla ilgili bol bol örnek için lütfen beni Twitter hesabımdan takip ediniz: @borsaninizinden
Ek olarak, sizler için hazırladığım Borsa Sözlüğünü gezmek için tıklayın!




